Irreducible component

In mathematics, the concept of irreducible component is used to make formal the idea that a set such as defined by the equation

XY = 0

is the union of the two lines

X = 0

and

Y = 0.

The notion of irreducibility is stronger than connectedness.

Definition

A topological space X is reducible if it can be written as a union 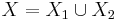$X = X_1 \cup X_2$ of two closed proper subsets 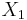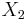$X_1$ , $X_2$ of $X$ . A topological space is irreducible (or hyperconnected) if it is not reducible. Equivalently, all non empty open subsets of X are dense or any two nonempty open sets have nonempty intersection.

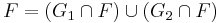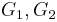A subset F of a topological space X is called irreducible or reducible, if F considered as a topological space via the subspace topology has the corresponding property in the above sense. That is, $F$ is reducible if it can be written as a union $F = (G_1\cap F)\cup(G_2\cap F)$ where $G_1,G_2$ are closed subsets of $X$ , neither of which contains $F$ .

An irreducible component of a topological space is a maximal irreducible subset. If a subset is irreducible, its closure is, so irreducible components are closed.

Use in algebraic geometry

In general algebraic variety or scheme X is the union of its irreducible components X_i. In most cases occurring in "practice", namely for all noetherian schemes, there are finitely many irreducible components. There is the following description of irreducible affine varieties or schemes X = Spec A: X is irreducible iff the coordinate ring A of X has one minimal prime ideal. This follows from the definition of the Zariski topology. In particular, if A has no zero divisors, Spec A is irreducible, because then the zero-ideal is the minimal prime ideal.

As a matter of commutative algebra, the primary decomposition of an ideal gives rise to the decomposition into irreducible components; and is somewhat finer in the information it gives, since it is not limited to radical ideals.

An affine variety or scheme X = Spec A is connected iff A has no nontrivial (i.e. ≠0 or 1) idempotents. Geometrically, a nontrivial idempotent e corresponds to the function on X which is equal to 1 on some connected component(s) and 0 on others.

Irreducible components serve to define the dimension of schemes.

Examples

The irreducibility depends much on actual topology on some set. For example, possibly contradicting the intuition, the real numbers (with their usual topology) are reducible: for example the open interval (−1, 1) is not dense, its closure is the closed interval [−1, 1].

However, the notion is fundamental and more meaningful in algebraic geometry: consider the variety

X := {x · y = 0}

(a subset of the affine plane, x and y are the variables) endowed with the Zariski topology. It is reducible, its irreducible components are its closed subsets {x = 0} and {y = 0}.

This can also be read off the coordinate ring k[x, y]/(xy) (if the variety is defined over a field k), whose minimal prime ideals are (x) and (y).

This article incorporates material from irreducible on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.

This article incorporates material from Irreducible component on PlanetMath, which is licensed under the Creative Commons Attribution/Share-Alike License.